Mit dem einfachen Z-Test oder Gauß-Test überprüft man anhand einer Stichprobe Vorstellungen über den Erwartungswert einer Grundgesamtheit.
Voraussetzungen
Der Z-Test kann verwendet werden, wenn eine normalverteilte Zufallsvariable mit unbekanntem Erwartungswert µ und bekannter Varianz ![]() vorliegt. Es wird dann geprüft, ob ein bestimmter Erwartungswert
vorliegt. Es wird dann geprüft, ob ein bestimmter Erwartungswert ![]() in Frage kommt. Unter gewissen Umständen kann auf die obigen Annahmen verzichtet werden.
in Frage kommt. Unter gewissen Umständen kann auf die obigen Annahmen verzichtet werden.
Z.TEST()-Funktion (rechtsseitiger Z-Test)
Bei Verwendung der Z.TEST()-Funktion in Google Tabellen wird standardmäßig ein rechtsseitiger Z-Test durchgeführt bzw. der Output der Z.TEST()-Funktion ist der p-Wert bei einem rechtsseitigen Test. Angenommen wir haben eine normalverteilte Zufallsvariable ![]() , beispielsweise die Körpergröße von Männern in cm. Wir wissen aus Erfahrung, dass die Standardabweichung 5 cm beträgt (
, beispielsweise die Körpergröße von Männern in cm. Wir wissen aus Erfahrung, dass die Standardabweichung 5 cm beträgt (![]() ). Nun liegt uns eine Stichprobe vom Umfang
). Nun liegt uns eine Stichprobe vom Umfang ![]() vor. Es ergibt sich eine durchschnittliche Körpergröße von
vor. Es ergibt sich eine durchschnittliche Körpergröße von ![]() . Es soll getestet werden, ob die Nullhypothese
. Es soll getestet werden, ob die Nullhypothese ![]() bei einem Signifikanzniveau von
bei einem Signifikanzniveau von ![]() beibehalten werden kann.
beibehalten werden kann.
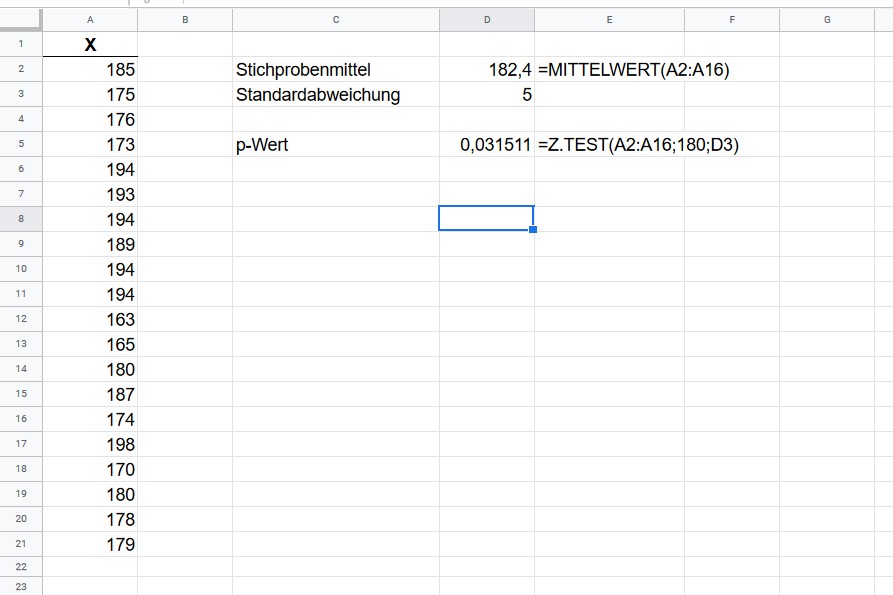
In der obigen Abbildung befindet sich in der Spalte A unsere Stichprobe. Das Stichprobenmittel ![]() berechnen wir ganz einfach mit der MITTELWERT()-Funktion für den Bereich A2:A16. In Zelle D3 steht die uns bekannte Standardabweichung in der Population. Und in Zelle D5 rechnen wir den p-Wert mit Z.TEST() aus.
berechnen wir ganz einfach mit der MITTELWERT()-Funktion für den Bereich A2:A16. In Zelle D3 steht die uns bekannte Standardabweichung in der Population. Und in Zelle D5 rechnen wir den p-Wert mit Z.TEST() aus.
Z.TEST() verlangt drei Parameter. Der erste Parameter sind die Daten unserer Stichprobe (A2:A16), der zweite Parameter ist quasi die Nullhypothese und der dritte die Standardabweichung. Falls man kein drittes Argument an die Funktion übergibt, so wird die Standardabweichung in der Population durch die Standardabweichung in der Stichprobe geschätzt. Dieses Vorgehen wäre bei einer normalverteilten Zufallsvariable, unbekannter Varianz in der Grundgesamtheit sowie einem ![]() vertretbar, da die Teststatistik in diesem Fall approximativ normalverteilt wäre.
vertretbar, da die Teststatistik in diesem Fall approximativ normalverteilt wäre.
In unserem Beispiel erhalten wir ![]() . Dies bedeutet, dass wir unter der Nullhypothese unser oder ein extremeres Ergebnis mit einer Wahrscheinlichkeit von
. Dies bedeutet, dass wir unter der Nullhypothese unser oder ein extremeres Ergebnis mit einer Wahrscheinlichkeit von ![]() erwarten können. Da der p-Wert geringer ist als unser Signifikanzniveau, verwerfen wir unsere Nullhypothese.
erwarten können. Da der p-Wert geringer ist als unser Signifikanzniveau, verwerfen wir unsere Nullhypothese.
Zweiseitiger Z-Test mit Z.TEST()
Nun wollen wir einen ungerichteten (zweiseitigen) Z-Test durchführen: ![]() . Das Signifikanzniveau von
. Das Signifikanzniveau von ![]() behalten wir bei. Aufgrund der Achsensymmetrie der Standardnormalverteilung müssen wir hierbei nur den Output von Z.TEST() mit 2 multiplizieren (Zelle D9).
behalten wir bei. Aufgrund der Achsensymmetrie der Standardnormalverteilung müssen wir hierbei nur den Output von Z.TEST() mit 2 multiplizieren (Zelle D9).
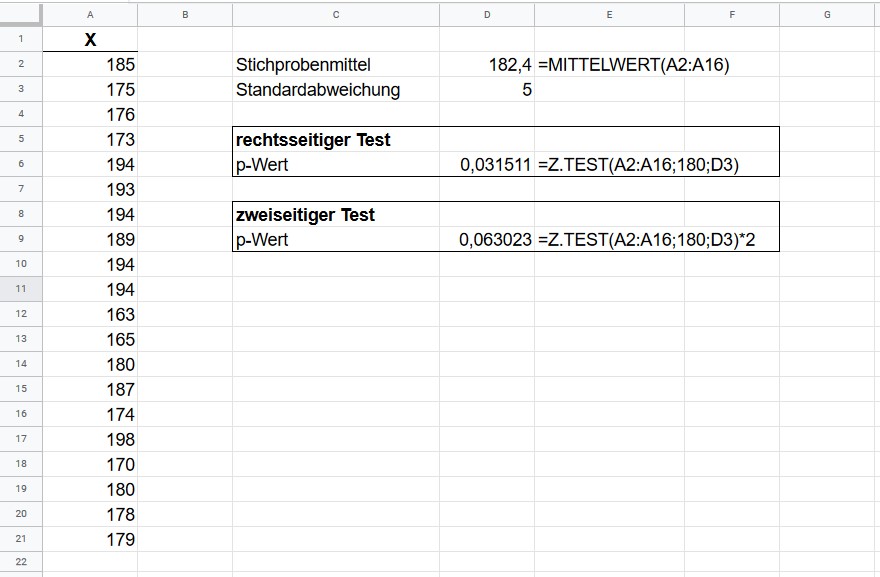
Der resultierende p-Wert ist nun größer als unser Signifikanzniveau und wir behalten in diesem Fall die Nullhypothese bei.
Linksseitiger Z-Test mit Z.TEST()
Für den linksseitigen Z-Test (![]() ) betrachten wir nun eine neue Stichprobe mit gleichem Umfang (
) betrachten wir nun eine neue Stichprobe mit gleichem Umfang (![]() ) aber einem neuen Mittelwert
) aber einem neuen Mittelwert ![]() . Das Signifikanzniveau
. Das Signifikanzniveau ![]() soll weiterhin
soll weiterhin ![]() betragen. Da Z.TEST() standardmäßig die Wahrscheinlichkeit für unseren Stichprobenmittelwert oder einen höheren Wert bei Geltung unserer Nullhypothese zurückgibt und wir gleichzeitig wissen, dass die Fläche unterhalb der Vergleichsverteilung
betragen. Da Z.TEST() standardmäßig die Wahrscheinlichkeit für unseren Stichprobenmittelwert oder einen höheren Wert bei Geltung unserer Nullhypothese zurückgibt und wir gleichzeitig wissen, dass die Fläche unterhalb der Vergleichsverteilung ![]() entspricht, können wir einfach die Gegenwahrscheinlichkeit dieses Ereignisses berechnen. Wir ziehen somit den Output von Z.TEST() von
entspricht, können wir einfach die Gegenwahrscheinlichkeit dieses Ereignisses berechnen. Wir ziehen somit den Output von Z.TEST() von ![]() ab.
ab.
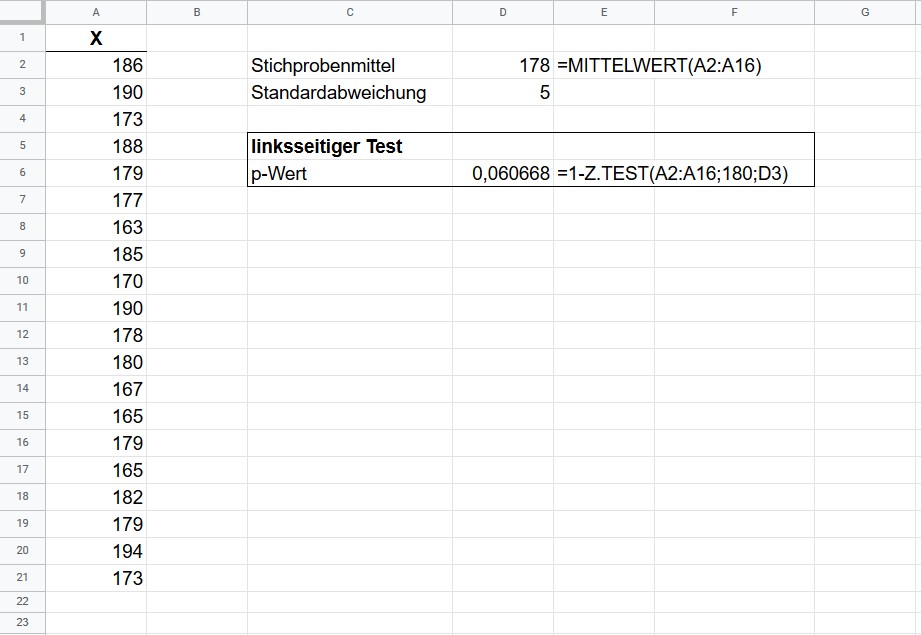
Für unser Beispiel erhalten wir nun einen p-Wert von ![]() . Dieser Wert ist größer als unser Signifikanzniveau und wir behalten die Nullhypothese bei.
. Dieser Wert ist größer als unser Signifikanzniveau und wir behalten die Nullhypothese bei.