Die einfache Lineare Regression wird verwendet um den linearen Zusammenhang zwischen einer erklärenden (bzw. unabhängigen oder exogenen) und einer zu erklärenden (bzw. abhängigen oder endogenen) Variable abzubilden. Davon zu unterscheiden ist die multiple lineare Regression, die mit mindestens zwei unabhängigen Variablen arbeitet. Im Folgenden soll nur die einfache lineare Regression mit Google Tabellen thematisiert werden, deren Ergebnis eine lineare Funktion mit zwei Parametern – dem y-Achsenabschnitt und der Steigung – ist.

Beispiel: Advertising-Datensatz

Für das folgende Beispiel werden wir den “advertising”-Datensatz aus “An Introduction to Statistical Learning” verwenden. Der Datensatz besteht aus den Verkaufszahlen (‘sales’) eines bestimmten Produktes in 200 verschiedenen Märkten. Gleichzeitig sind die dazugehörigen Werbebudgets für drei verschiedene Medien (‘TV’, ‘Radio’ und ‘Newspaper’) angegeben. Uns soll es hierbei vor allen Dingen um die Anwendung der linearen Regression in Google Tabellen gehen.¹

Zusammenhänge visualisieren: Streudiagramm

Wir wollen nun herausfinden ob eine Beziehung zwischen dem Budget für TV-Werbung und den Verkaufszahlen besteht. Dazu fertigen wir zunächst ein Streudiagramm (Scatterplot) für die beiden Variablen an. Das Werbebudget wird dabei als erklärende Variable auf der x-Achse abgetragen und die ‘sales’ auf der y-Achse.

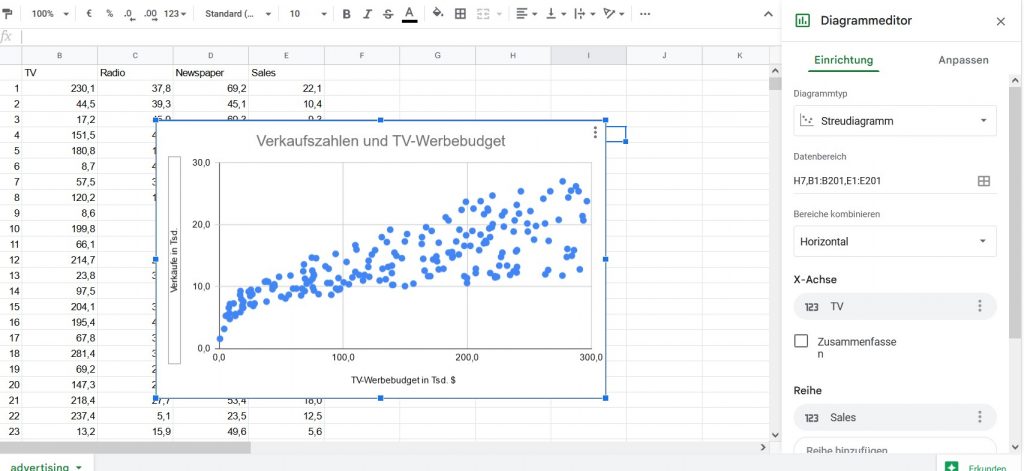
Im Scatterplot kann man einen erwartbaren positiven Zusammenhang zwischen Werbeausgaben und Verkaufszahlen ausmachen. Höhere TV-Werbebudgets gehen einher mit höheren Verkaufszahlen. Wir wollen nun die beiden Parameter des folgenden Modells schätzen:

   

Hierbei repräsentiert den Achsenabschnitt und die Steigung einer Geraden, welche durch die Punktwolke verläuft. Diese sogenannte Regressionsgerade hat im Vergleich zu allen anderen möglichen Geraden die Eigenschaft, dass die Summe der quadrierten Abstände zwischen den Punkten und der Geraden minimal ist. Daher wird der Weg zu dieser Geraden auch als Methode der kleinesten Quadrate bezeichnet.

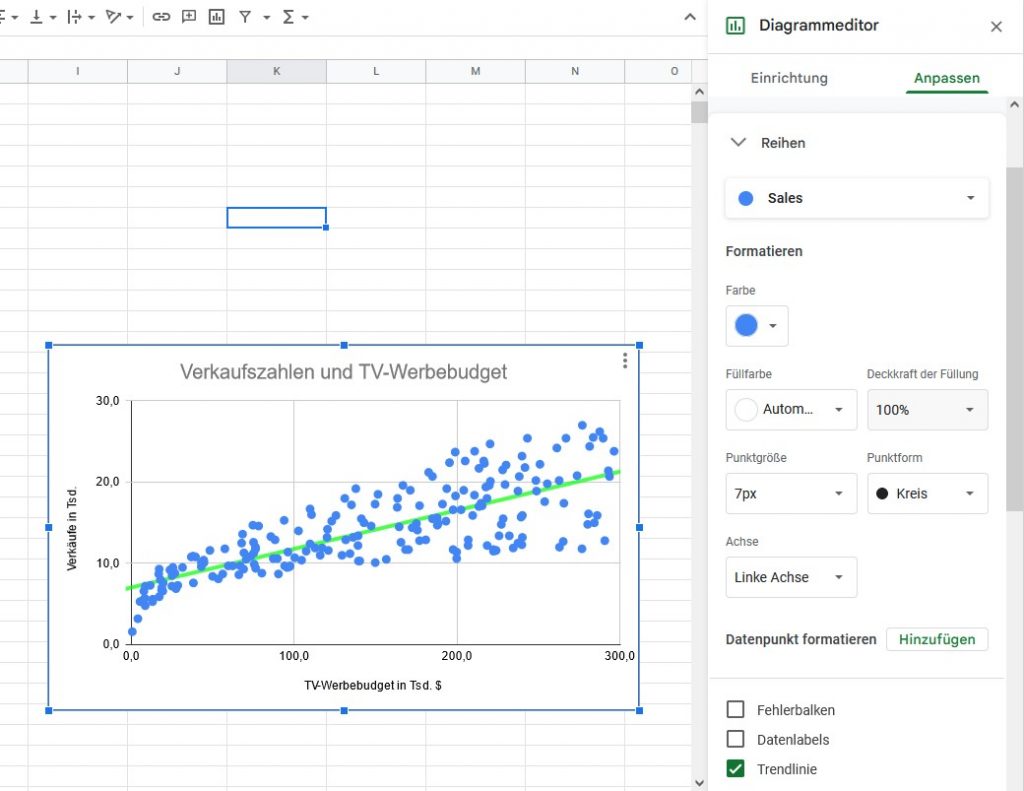
Graphisch lässt sich diese Regressionsgerade übrigens sehr simpel dem bereits erstellten Streudiagramm hinzufügen. Im Diagrammeditor geht man unter dem Punkt “Anpassen” zuerst auf “Reihen” und markiert dann den Punkt “Trendlinie”.

Schätzung der Parameter mit RGP()

Nun sollen die Steigung und der y-Achsenabschnitt der Regressionsgeraden mit der RGP()-Funktion berechnet werden. Die RGP()-Funktion kann mit vier Parametern benutzt werden.

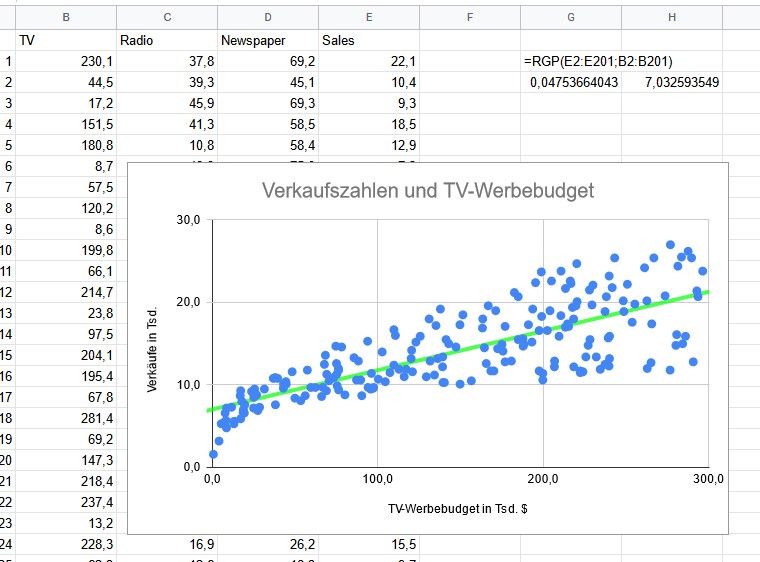
Für unsere einfache lineare Regression geben wir jedoch nur die ‘Sales’-Daten in Spalte E (zu erklärende Variable) als “bekannte_Daten_y” und die TV-Werbebudget-Daten (erklärende Variable) als “bekannte_Daten_x” an die Funktion (Zelle G3) weiter und erhalten dann die gewünschten Funktionsparameter als Output. Sollten wir die Schätzung ohne Interzept (also einem y-Achsenabschnitt bei 0) durchführen wollen, müssten wir als drittes Argument “FALSCH” für ‘b’ angeben. Und einen ausführlicheren Output mit Informationen zur Regression erhalten wir über die Eingabe von “WAHR” als viertes Argument.

Wir bleiben jedoch beim nicht ausführlichen Output mit Interzept. In Zelle G3 sehen wir nun die Steigung (0,0475) und in Zelle H3 den y-Achsenabschnitt (7,0326). Diese Parameter stimmen natürlich genau mit jenen überein, die Google Tabellen für die Zeichnung der Trendlinie verwendet hat.

---

1. Für eine detaillierte Betrachtung der einfachen linearen Regression siehe z.B. James, G. et al. (2021): An Introduction to Statistical Learning with Applications in R, 2nd edition, S. 60-71 oder Assenmacher, W. (2002): Einführung in die Ökonometrie, 6. Aufl., München, S. 81-87.